The estat hettest Command
This command performs the Breusch-Pagan and Cook-Weisberg test for heteroskedasticity in a linear regression model. This command works off the null hypothesis that variance is homoskedastic. If variance is homoskedastic this means that the variance for each observation is around the same finite value (i.e. variance is uniform). If a linear regression contains heteroskedasticity, we are saying that rather than a uniform variance, the variance is influenced by one or more variables.
Due to the fact that linear regression assumes homoskedasticity, a heteroskedastic model violates this assumption. Since we usually want to be able to use significance tests in our model to make inferences about our data, we test for heteroskedasticity to make sure our inferences are not baseless.
This particular test looks specifically for cone-shaped heteroskedasticity in a linear regression. Cone-shaped heteroskedasticity starts with a small amount of variance at the beginning of the regression line, with variance increasing as the line progresses. This ends in a large amount of variance at the end of the regression line. In other words, higher variances are linked with higher (or lower if the regression line is negative) values in a particular variable. See the graph below which shows a regression line and the variance around it.

To test for other types of heteroskedasticity (e.g. hourglass shaped) try the estat imtest and estat szroeter commands.
Please bear in mind that this test for heteroskedasticity assumes that the residuals are normally distributed. If the residuals in your model are not normally distributed then this test will be biased.
How to Use:
*Perform linear regression, then
estat hettest
OR to test all independent variables simultaneously
estat hettest, rhs
OR to test a single independent variable
estat hettest var1
OR to test all independent variables and score them
estat hettest, rhs mtest(chosen_adjustment)
Worked Example:
In this example I use the auto dataset. I am going to generate a linear regression, and then use estat hettest to test for heteroskedasticity. In the command pane I type the following:
sysuse auto, clear
regress price mpg rep78
estat hettest
From this I get the following output:

Here you see the Stata output for the regression followed by the test for heteroskedasticity. The default for estat hettest uses the fitted values of the dependent variable to test for heteroskedasticity. This default test generated a p-value of 0.0106 which, as it is less than my chosen significance value of 0.05, indicates a statistically significant Chi-square test. This result indicates the presence of heteroskedasticity in the dependent variable price.
One way of dealing with heteroskedasticity related to a particular variable is to transform that variable in such a way that it changes the relationship with the residuals. One of the more common ways to transform a variable is to create a new variable containing the natural logarithmic values of the variable. To do this in Stata we use the log() function when generating or replacing a variable. Lets transform price and re-run our regression and heteroskedasticity test to see if transforming our dependent variable has an effect. in the command pane type the following:
generate ln_price = log(price)
regress ln_price mpg rep78
estat hettest
This gives the following output:

This second regression has returned a p-value of 0.1017 for the heteroskedasticity test. This test is no longer significant as the p-value is greater than our chosen 0.05 cutoff. This suggests that our log transformation of the dependent variable price has successfully eliminated problems with heteroskedasticity.
Note: You should be very careful when using a model that contains transformed variables such as this. The linear relationships in this model are now indicative of the natural logarithm of price, and not the underlying values of price itself. This can make interpreting your model more difficult, so make sure the transformation you use will still give you a meaningful result.
Now I also want to test for heteroskedasticity in the independent variables. To do this I type the following in the command pane:
estat hettest, rhs

This test is looking for heteroskedasticity linked to all independent variables, rather than the fitted values of the dependent variable. With a p-value of 0.1809 the test indicates there is no significant heteroskedasticity related to our independent variables. However, this is a test that looks at all independent variables together. By testing all independent variables at once you can end up with a situation where homoskedasticity is masking heteroskedasticity.
If you have a model with a small number of independent variables, or are particularly concerned about specific variables, you can test each individually. Alternatively, you can run a multiple-hypotheses test by specifying a multiple-testing adjustment in addition to the rhs option. If you test multiple hypotheses at once, the likelihood you will incorrectly reject the null hypothesis (make a false positive or type 1 error) increases with each additional test. You need to adjust the p-values of your multiple tests to take this into account.
Stata allows three different adjustments. The first is the Bonferroni correction, which controls for type 1 errors as well as the per-family type 1 error rate. The Bonferroni correction is specified using the mtest(bonf) option. The second adjustment is the Holm-Bonferroni method, which is always more powerful, or at least as powerful, as the Bonferroni correction. However, unlike the Bonferroni correction, this method does not control for the family type 1 error rate. The Holm-Bonferroni method is specified using the mtest(holm) option. The third adjustment allowed by Stata is the Sidak correction. The Sidak correction is more powerful than the other two adjustments only when the hypothesis tests are not negatively dependent (i.e. independent or positively dependent). The Sidak correction is specified using the mtest(sidak) option. You can also specify that you do not want adjusted p-values with the mtest(noadjust) option.
As we only have two independent variables in our model we can test each of them independently, as well as together using a multiple-test adjustment. I will first test each of them independently, before testing all independent variables together using the Bonferroni correction. In the command pane I type the following:
estat hettest mpg
estat hettest rep78
estat hettest, rhs mtest(bonf)
From this I get the following output:

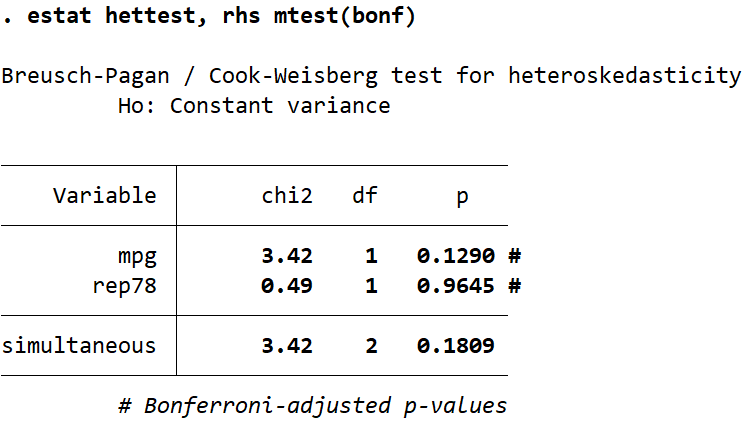
None of these tests are statistically significant given a p-value cutoff of 0.05, however you should note the difference in the p-values when individually tested versus multiple-testing with the Bonferroni correction.
This test is quite narrow in terms of the heteroskedasticity it can detect, and its usefulness is dependent on your model having normally distributed residuals. It is possible for this model to contain heteroskedasticity of a different form that is remaining undetected. There are other tests for heteroskedasticity, such as estat imtest and estat szroeter, that can detect different forms of heteroskedasticity.
Additionally, the residuals in this model do not appear normally distributed when plotted. Had I been running this regression as part of an analysis, I would have checked the distribution of residuals first, and would not have run this estat hettest test having identified non-normality in the distribution.