The predict Command - Linear Regression Post-estimation
The predict command can be used in many different ways to help you evaluate your regression model. Here we will cover it’s use in relation to linear regressions. For linear regressions you can use predict to generate variables containing the following:
Additionally, if you run a regression model with offset or exposure variables you can use the nooffset option to have predict ignore these when generating any of the above items. And if you do not want Stata to add a variable label to your predict generated variables use the nolabel option.
How to Use:
*To generate model-predicted values of the dependent variable (fitted values)
predict newvarname, xb
*To generate a variable containing the residuals
predict newvarname, residuals
*To generate a variable containing standardised residuals
predict newvarname, rstandard
*To generate a variable containing studentised (jackknifed) residuals
predict newvarname, rstudent
*To generate a variable containing the standard error of the model prediction (fitted values)
predict newvarname, stdp
*To generate a variable containing the standard error of the residuals
predict newvarname, stdr
*To generate a variable containing the standard error of the forecast
predict newvarname, stdf
*To generate a variable containing the leverage values for each observation
predict newvarname, leverage
*To generate a variable containing the DFITS influence statistic
predict newvarname, dfits
*To generate a variable containing the Cook’s D influence statistic
predict newvarname, cooksd
*To generate a variable containing the Welsch D influence statistic
predict newvarname, welsch
*To generate a variable containing the COVRATIO influence measure
predict newvarname, covratio
Worked Example 1 - Linear Model Predictions:
In this first example I am going to use the auto dataset to run a linear regression and generate the fitted values for that regression. I will then plot those against the dependent variable to see how well the predictions hold up. In the command pane I type the following:
sysuse auto, clear
regress mpg weight price
predict mpg_fitted, xb
scatter mpg_fitted mpg
This gives the following regression output, followed by a scatter graph as shown below:

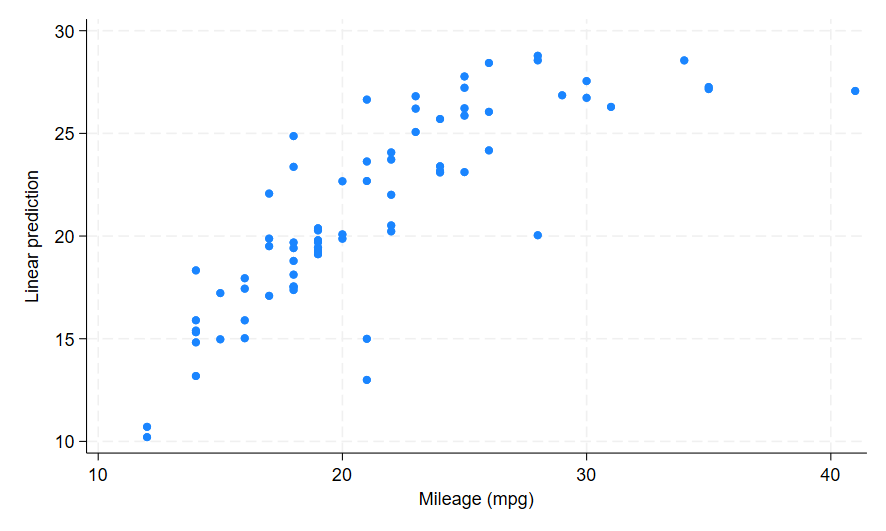
My predicted variable mpg_fitted contains the linear model prediction values of the dependent variable mpg. Looking at the scatter my prediction appears curved, and it does not cover the full range of the original mpg values as it has a smaller axis range.
Also note the predict command has added the label Linear prediction to my mpg_fitted variable, which is visible along the x-axis. If you do not want a variable label, you can add the nolabel option along with any of the other predict options and Stata will not add its default label.
Worked Example 2 - Residuals:
For this example I am going to use the predict command to create variables containing the original residuals, standardised residuals, and studentised residuals of my regression. I am then going to use the histogram command to look at the distribution of each of these residual variables. One of the underlying assumptions of a linear regression is that the residuals will have a normal distribution, and this is one way of visually evaluating if that is true for your model. In the command pane I type the following:
sysuse auto, clear
regress mpg weight price
predict resid, residuals
histogram resid, frequency normal
Here is the regression, followed by a histogram of the residuals:

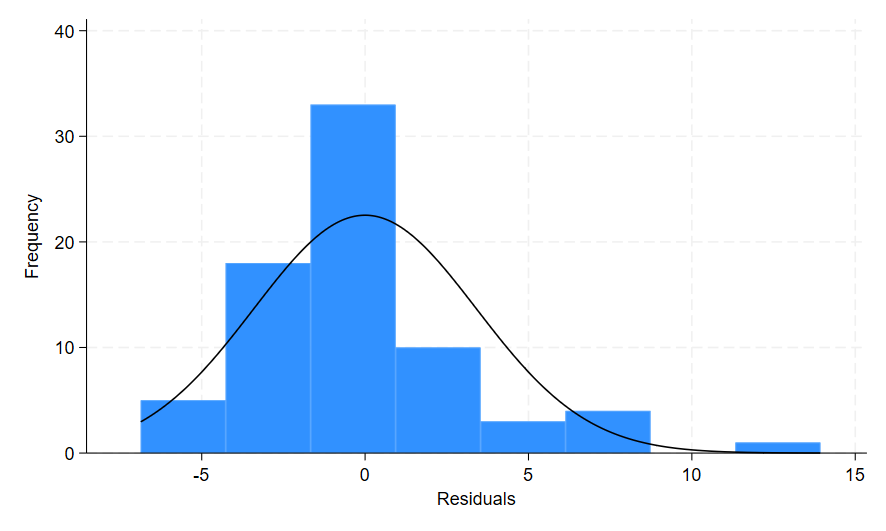
The option residuals added to the predict command generated a new variable resid that contains the residual values for my model. When I ran the histogram command, I added the option frequency because I wanted the count data rather than the density on the y-axis. The normal option added a curve on top of the histogram to represent a normal distribution. This allows me to compare the histogram bars to the normal distribution line to help determine if my residuals are normally distributed.
The distribution of the residuals in this histogram looks mostly ok, although they appear a bit skewed and the bars in the middle are higher than the curve indicating some kurtosis.
Now let’s have a look at the standardised and studentised residuals as well. In the command pane I type the following:
predict resid_standard, rstandard
predict resid_student, rstudent
histogram resid_standard, frequency normal
histogram resid_student, frequency normal
This produces the following two histograms:
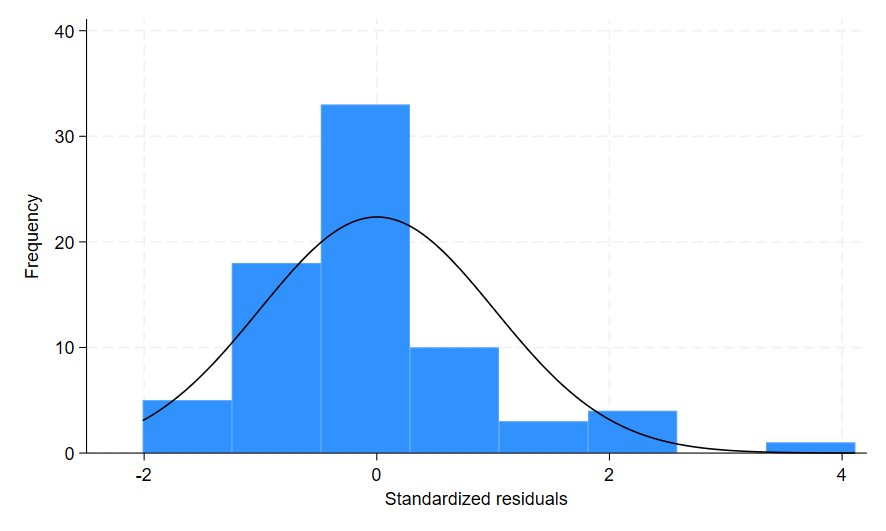
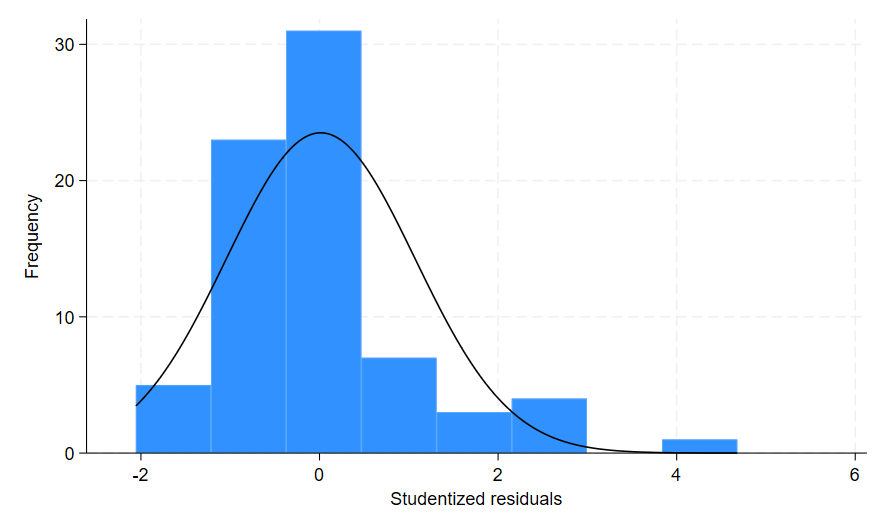
The first histogram shows the standardised residuals from the variable resid_standard, and the second histogram shows the studentised residuals from the variable resid_student. The x-axis shows the variable label by default, and again predict has labelled the variables according to what was calculated. If you prefer the English spelling of these words you can use the nolabel command and then simply label your predict-generated variables how you choose.
Worked Example 3 - Standard Errors:
For this example I am going to use the predict command to generate variables containing the standard error of the model prediction (fitted values), the standard error of the forecast, and the standard error of the residuals. The standard error of the forecast can be considered the sum of the prediction error and residual error. For this reason the standard error of the forecast is always larger than the standard error of the prediction.
The standard error you use when evaluating your predictions will depend on what you are using your prediction for. If you are creating a prediction within-sample (i.e. on data that was used to generate the model prediction) then only the standard error of the prediction is necessary. However if you are using your prediction out-of-sample (i.e. on data that is separate and was not used to create the model prediction), then you need to use the standard error of the forecast.
Let’s start by looking at the standard error of the prediction. In the command pane I type the following:
sysuse auto, clear
regress mpg weight price
predict mpg_fitted, xb
predict ste_fitted, stdp
list make mpg mpg_fitted ste_fitted in 1/2
The regression (as before) is below, followed by the first two cars in the dataset:
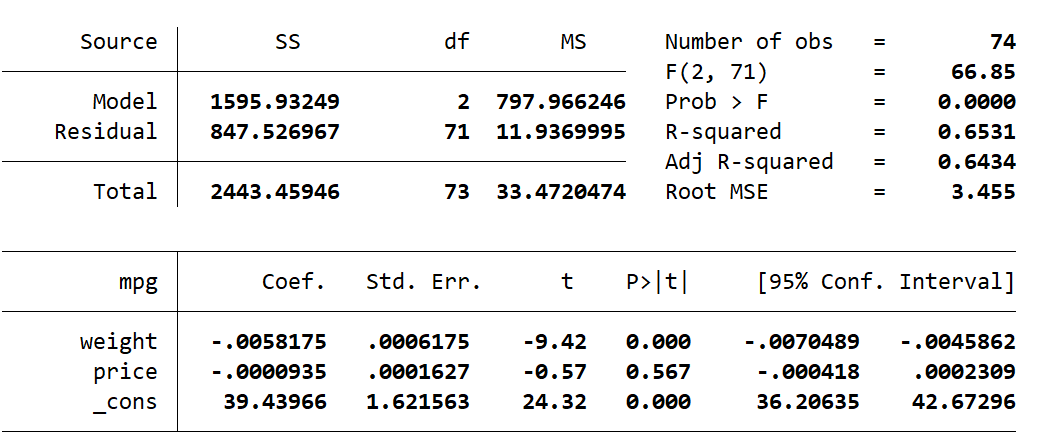
Here you can see the true mpg value, the predicted mpg value, and the standard error of the prediction. This means the Concord has a predicted mpg of 22.01 ± 0.51 and the Pacer has a predicted mpg of 19.51 ± 0.55. This is a range of 21.5 to 22.52 predicted mpg for the Concord, and a range of 18.96 to 20.06 for the Pacer.
Now let’s take a look at the residuals. In the command pane I type the following:
predict resid, residuals
predict ste_resid, stdr
list make resid ste_resid in 1/2
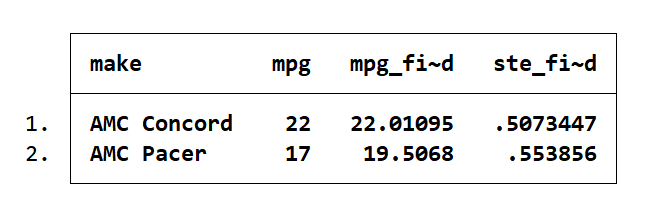
The residual is the difference between the actual (mpg) and predicted (mpg_fitted) values of the dependent variable. The standard error indicates the error in that calculation. For the Concord the residual is -0.011 ± 3.42, and for the Pacer the residual is -2.51 ± 3.41. This is a range of -3.43 to 3.43 for the Concord and a range of -5.92 to 0.90 for the Pacer.
Now let’s have a look at the standard error of the forecast. To do this I am going to use the input command to create a small 2-car dataset using a Mazda 3 car and a Honda Accord car. For the comparison to be reasonable I will need to transform the price of the cars today to take into account the US$ inflation rate since 1978.
This website tells me that $1 in 1978 is equivalent to $3.97 today (in 2020). So I will divide the current price by 3.97 to get the approximate price of that car if it were on the market in 1978. For the Mazda the current US$ price for a Mazda 3 Sedan is $21,500. The 1978 equivalent price for the Mazda is $5,416 (21500/3.97). The current price for the Honda Accord is $24,020. The 1978 equivalent price for the Honda is $6,050 (24020/3.97).
Once my 2-car dataset is made I can use the previously fit regression model on this new dataset with the predict command. In the command pane I type the following:
clear
input str20 make mpg weight price
"Mazda 3 Sedan" 37.9 2950 5416
"Honda Accord" 36.2 3316 6050
end
predict mpg_fitted, xb
predict ste_forecast, stdf
list make mpg mpg_fitted ste_forecast
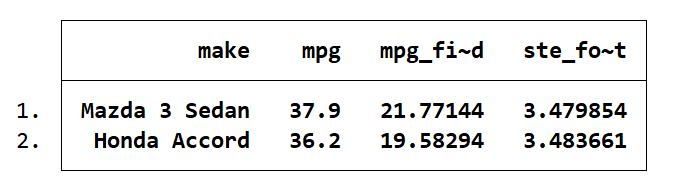
Here you can see the predicted mpg for the Mazda is 21.77 ± 3.48, and for the Honda it is 19.58 ± 3.48. This is an mpg range of 18.29 to 25.25 for the Mazda, and for the Honda an mpg range of 16.1 to 23.06. These predicted mpg ranges are far below the actual mpg values for these cars. This is because I am using the model to make predictions about modern cars. These cars have the benefit of significant automotive advancements that make them much more fuel efficient than cars from the 1970s. Since the dataset I used to generate my model contains cars exclusively from 1978, it is not really applicable to modern automobiles.
Worked Example 4 - Leverage, DFITS, Cook's D, Welsch D and COVRATIO:
For this final example I will use the predict command to generate leverage values, as well as the DFITS, Cook’s D, Welsch D and covratio influence statistics. The influence statistics are all attempts at combining the leverage and residual values into a single numeric representation.
Both leverage and residual values can indicate outliers or problem observations. An observation with high leverage is a lonely observation – there are no surrounding observations to provide corroboration. This means observations with high leverage are pulling the regression line towards them. An observation with a high residual is an outlier – the predicted value of the dependent variable is very different from the true observed value. This means observations with high residual values sit far away from the regression line.
An observation with a high influence value (from DFITS, Cook’s D, Welsch D or Covratio) can be influential because it has high leverage, or it has a high residual, or it has high values for both leverage and residual. An observation that has both high leverage and a high residual is both lonely and an outlier. All three kinds of observation (lonely, outlier, or both) should be identifiable to some degree in the influence statistics.
For this example I will use the predict command to generate a variable containing leverage, as well as variables containing the four influence statistics. As stated in the Stata base reference manual, there is a cut-off value to help identify problematic observations from the influence statistics. Any observation with a value above the cut-off is worthy of further investigation. Each statistic has its own cut-off which I will list below. For leverage, rather than using a cut-off I will look at any observations with leverage values in the top 5% of all leverage values.
For each of these calculations the letter k is the number of independent variables (including the constant) in the model, and the letter n is the number of observations in the model.
For the following example I will create each of these cut-offs as local macros so I can easily reference them when I want to list observations.To create the macro cut-offs easily I am going to use a couple of Stata temporary macro values.
When you run an estimates command such as regress in Stata the number of variables (including constant) and the number of observations in the model are saved as temporary values. I will use these temporary values to easily create my cut-offs without having to look them up. The value for k is saved as e(rank) and the value for n is saved as e(N). You will notice these two values substituted for k and n in the appropriate cut-off calculations in my example below. Stata also creates temporary macro values for other commands such as summarize. I use the r(p95) temporary value from summarize to easily look at observations in the top 5% of leverage values.
Please note: when calling macros the opening single quote is not the same as the closing single quote. The opening single quote is the grave, which is located on the tilde (~) key next to 1 on your QWERTY keyboard. The closing single quote is as normal, on the double quote key.
In the command pane I type the following:
sysuse auto, clear
regress mpg weight price
This is the same regression that we have used in previous examples, shown below:
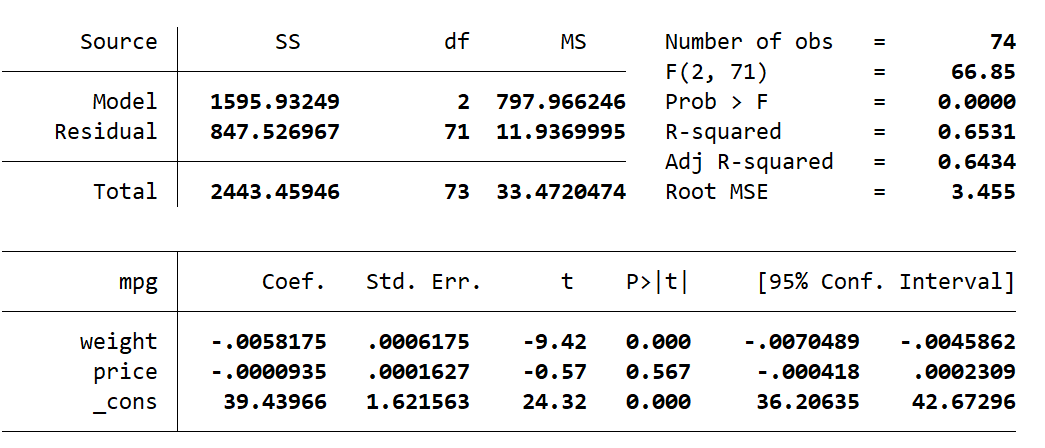
Now I will create the leverage variable and use the summarize command with the detail option to look at any observations with a leverage in the top 5% of leverage values. In the command pane I type the following:
predict leverage, leverage
summarize leverage, detail
local leverage_cutoff = r(p95)
display `leverage_cutoff'
list make mpg weight price leverage if leverage > `leverage_cutoff'
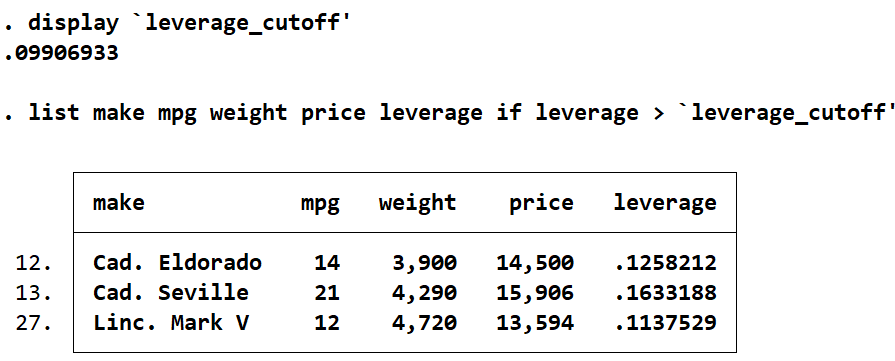
These three cars have the top 5% of leverage values for this model. Note that the prices and weights of these cars are all on the high end for this dataset. The mean weight for cars in this dataset is 3019 lbs, and the maximum weight is 4840 lbs. The mean price for cars in this dataset is $6,165, and the maximum price is $15,906. All three cars are closer to the maximum values for weight and price than they are to the mean values. This is the most likely reason for their high leverage values.
Now let’s have a look at the influence statistics, starting with DFITS. In the command pane I type:
predict dfits, dfits
local dfit_cutoff = 2*sqrt(e(rank)/e(N))
display `dfit_cutoff'
list make mpg weight price dfits if dfits > `dfit_cutoff'

From the three cars we identified with high leverage values, only one of them appears here. As well as its high leverage the Cadillac Seville has the highest DFITS value. It’s DFITS value is more than double our cut-off of 0.4027. The Volkswagen Diesel also has a DFITS value that is more than double our cut-off. Both these cars warrant further investigation based on this statistic. The Datsun 210 and the Subaru have DFITS only a little higher than the cut-off, so they are not much of a concern here.
Now let’s move on to the Cook’s D influence statistic. In the command pane:
predict cook, cooksd
local cook_cutoff = 3/e(N)
display `cook_cutoff'
list make mpg weight price cook if cook > `cook_cutoff'
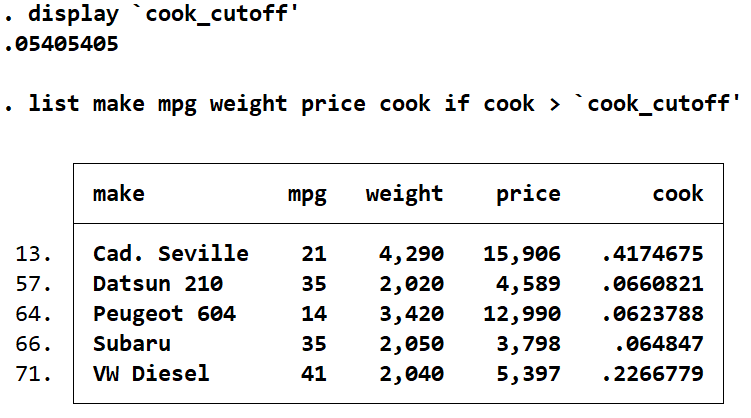
The four cars with high DFITS also appear with high Cook’s D statistics, with an addition of the Peugeot 604. As before with DFITS, the Cadillac Seville and Volkswagen Diesel have very high Cook’s D values. Here the high values are more pronounced, with the Cadillac Seville almost eight times higher than the cut-off and the Volkswagen Diesel more than four times higher than the cut-off. As before with DFITS, the Datsun 210 and the Subaru are only just above the cut-off along with the Peugeot 604. I am still really only concerned about the Cadillac and the Volkswagen.
Let’s move on to the Welsch D statistic. In the command pane:
predict welsch, welsch
local welsch_cutoff = 3*sqrt(e(rank))
display `welsch_cutoff'
list make mpg weight price welsch if welsch > `welsch_cutoff'
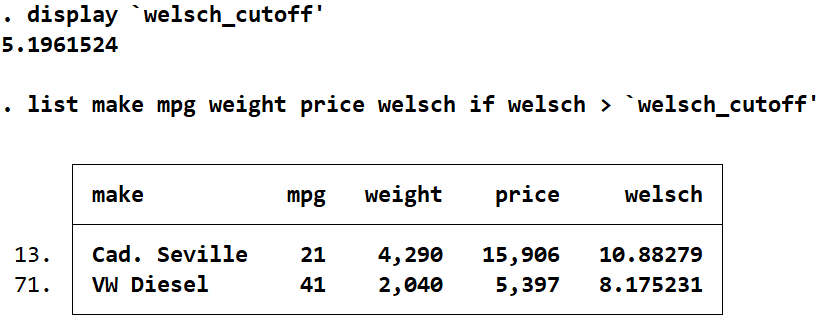
This time only the Cadillac Seville and the Volkswagen Diesel are identified. This is consistent with what we’ve seen from our DFITS and Cook’s D statistics. Similarly to DFITS, the Cadillac Seville is more than double the cut-off and the Volkswagen Diesel is only a bit less than that. Of all our statistics the Welsch D appears to be the strictest. If I had a dataset with many more observations, I may be more inclined to use the Welsch D statistic over the others.
Let’s have a look at our final influence statistic, COVRATIO. In the command pane I type:
predict cov, covratio
local cov_cutoff = (3*e(rank))/e(N)
display `cov_cutoff'
list make mpg weight price cov if abs(cov-1) >= `cov_cutoff'
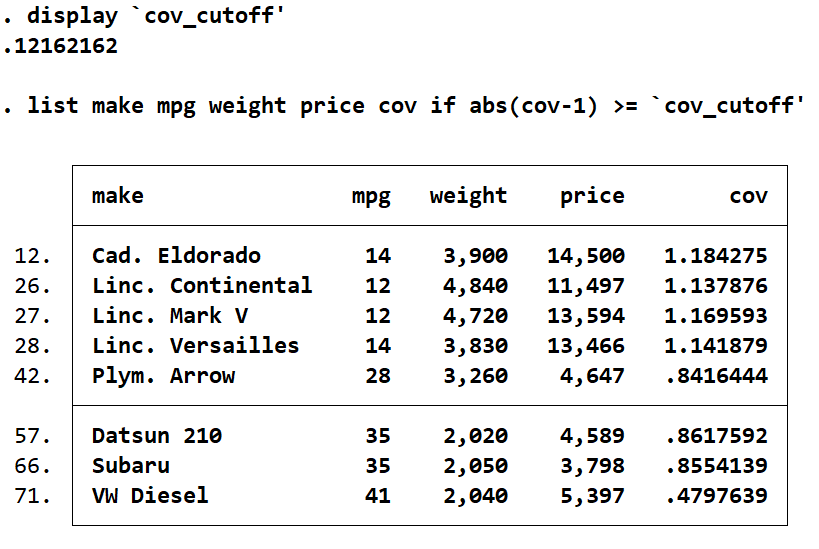
The COVRATIO statistic has identified more cars than any other influence statistic. It has a combination of cars we saw with high leverage, and those with high values in other statistics, as well as a few additions of its own. However, there is one glaring omission. The Cadillac Seville, identified as having the highest values on all other statistics and the highest leverage, is not identified by Covratio.
From what we have seen through the previous influence statistics and leverage, the Cadillac Seville has both a high leverage and a high residual. This makes it a very problematic observation, but it also makes it less likely to be identified by Covratio. For most normal noninfluential observations the Covratio value is approximately 1. Large values of residuals or large values of leverage will cause the Covratio to deviate from 1, which is what we look for with our cut-off. Any covratio value that is higher than 1 + cut-off, or lower than 1 – cut-off, is considered overly influential. But for observations with high leverage and high residual values, there is a tendency for their Covratio to trend back to 1. This causes it to be misidentified by the Covratio influence measure. For this reason, it is a good idea to use Covratio along with other influence statistic measures so you do not miss out on identifying observations that are lonely outliers.
It appears there is a problem with the Cadillac Seville and the Volkswagen Diesel. These observations deserve to be scrutinised, although we will not do so here.
I have covered all the different variables you can use predict to create for linear regressions. There are other things predict can be used for in other kinds of models, but I will not cover these here. If you are interested to see a future post deal with other uses of the predict command, let me know what you’d like me to cover by emailing me at sales@surveydesign.com.au.