Getting Started in Stata - The Chi-Square Test
In Stata there are many different significance tests that will use a chi-square test to report a p-value. For example, the estat hettest command uses a chi-square to determine the likelihood of heteroskedasticity in a regression model. To perform your own chi-square test in Stata you will need two categorical variables saved in a Stata dataset.
Today we are going to show you how to perform a standard Pearson’s chi-square test in Stata, using both drop-down menus and Stata commands. As a new Stata user it is recommended that you start by using the Stata menus to perform your analysis. Each analysis, such as a chi-square test, will show up in your Review pane (on the left side of the Stata screen) as the equivalent Stata command. This allows you to begin learning the general structure of commands and how to use them. Once you become more familiar with commands you will find it is faster and easier to perform your analyses using commands.
I am going to use the Stata Example dataset auto.dta. I load this dataset using the following command:
sysuse auto.dta
Pearson's Chi-Square via Stata Menus:
Statistics > Summaries, tables and tests > Frequency tables > Two-way table with measures of association

Select “rep78” under Row variable
Select “foreign” under Column variable
Click on “Pearson’s chi-squared” under the Test statistics box on the left side (make sure the box is ticked)
Click OK
Pearson's Chi-Square via Stata Commands:
tabulate rep78 foreign, chi2
Output:
Stata prints the following to the Results pane (in the centre of the Stata window):
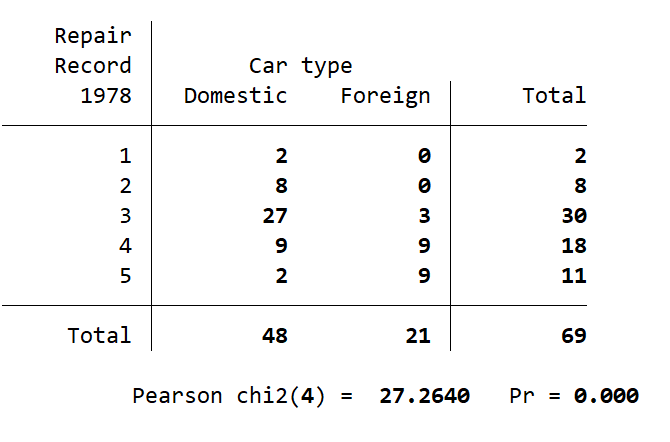
For this example I have performed a chi-square test on the “rep78” and “foreign” categorical variables. As the chi-square is run through the tabulate command in Stata the standard output is to provide a count breakdown across the rep78 and foreign variables. Below this table is the results of the chi-square test. The number in brackets after “Pearson chi2” is the degrees of freedom for this test, which is 4 in this case. The number after “Pearson chi2(4) =” is the chi-square value generated by the test. The number after “Pr =” is the p-value.
This example chi-square test has given a p-value of 0.000. In Stata this does not mean the p-value was zero, but rather it was less than 0.00005 and so Stata has rounded down. If you would like to see the actual p-value generated by the test you can use the command return listto list the values Stata saved when it ran the test. The value printed next to “r(p) =” in the Results pane is the actual p-value the chi-square test generated.
Please note that these special r values will change after each command you run in Stata. If you want to see the p-value associated with this test, the return list command must be run immediately after running the chi-square test. I ran the return list command in Stata after the test above and it gave the following output:

From this we can see our p-value was 0.0000175… which is not quite zero, but pretty close to it. From an analysis perspective it doesn’t much matter to me if my p-value is actually zero, or only almost zero. How I proceed in my analysis will not change. However, when reporting results it is best to give the actual value rather than an approximate value.
If you would like more information about your chi-square, you can also have Stata report the chi-square values within the table. If you are going through the menus, additionally select “Pearson’s chi-squared” from the Cell contents box on the right side of the menu box (pictured above). If you are using the command line, add the option “cchi2” to your command, so tabulate rep78 foreign, chi2 becomes tabulate rep78 foreign, chi2 cchi2. This will print the same table as above with the addition of the chi-square values printed beneath the count values.
When running this test on your own data, make sure to replace the variable names shown above with your own variables. Also, make sure you are using categorical variables for this test. If you have a continuous variable you want to use with this test you will first need to transform it into a categorical variable. See The Cut Function tech tip for information on how to separate a continuous variable into a categorical one.