The estat szroeter Command - Linear Regression Post-estimation
The estat szroeter command is a rank test for heteroskedasticity, which is an alternative to the score test used in estat hettest. The szroeter test evaluates the alternative hypothesis that variance increases monotonically in the variables tested. Monotonic simply means one-way. If you have variance that is increasing monotonically, it means it is never decreasing. The variance may increase as the linear regression line increases, and then at some point stop increasing and stay the same. As long as it does not decrease at any point it is considered monotonic.
This estat szroeter command tests the independent variables of a linear regression. You can test a single variable, or multiple named variables, or all independent variables, depending on the options specified. If you test multiple hypotheses at once, the likelihood you will incorrectly reject the null hypothesis (make a false positive or type 1 error) increases with each additional test. You will need to adjust the p-values of your multiple tests to take this into account.
Stata allows three different adjustments. The first is the Bonferroni correction, which controls for type 1 errors as well as the per-family type 1 error rate. The Bonferroni correction is specified using the mtest(bonf) option. The second adjustment is the Holm-Bonferroni method, which is always more powerful, or at least as powerful, as the Bonferroni correction. However, unlike the Bonferroni correction, this method does not control for the family type 1 error rate. The Holm-Bonferroni method is specified using the mtest(holm) option. The third adjustment allowed by Stata is the Sidak correction. The Sidak correction is more powerful than the other two adjustments only when the hypothesis tests are not negatively dependent (i.e. they are independent or positively dependent). The Sidak correction is specified using the mtest(sidak) option.
If you do not specify a multiple-test adjustment the default for this test will leave the p-values unadjusted. It is highly recommended you use some form of adjustment when you are running this test on many variables at once.
How to Use:
*Perform linear regression, then
To test all independent variables unadjusted
estat szroeter, rhs
OR to test specific named variables (you can test a single variable this way)
estat szroeter var1 var2 var3
OR to test all independent variables with an adjustment
estat szroeter, rhs mtest(chosen_adjustment)
OR to test specific named variables with an adjustment
estat szroeter var1 var2 var3, mtest(chosen_adjustment)
Worked Example:
In this example I use the auto dataset. I am going to generate a linear regression, and then use estat szroeter to test for heteroskedasticity. In the command pane I type the following:
sysuse auto, clear
regress price mpg rep78 weight length foreign
estat szroeter, rhs mtest(holm)
This gives the following output:

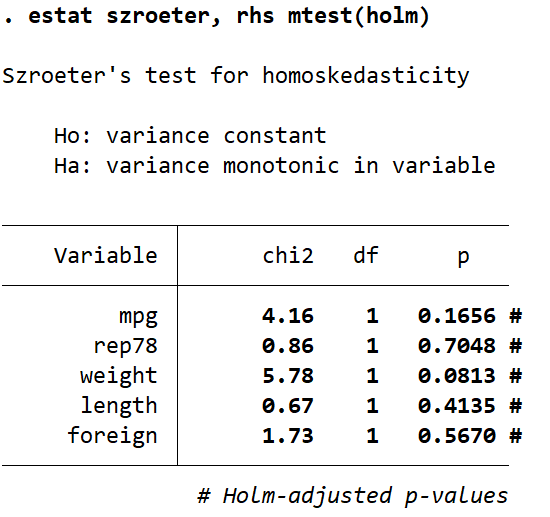
Using a significance cutoff of 0.05 we see no statistically significant heteroskedasticity in any of our independent variables. The mpg and weight variables have the lowest Holm-adjusted p-values, so lets re-run the test to only look at those. This time I’ll use a Bonferroni correction instead to demonstrate. In the command pane I type the following:
estat szroeter mpg weight, mtest(bonf)
This gives the following output:

The p-values for both variables are lower than they were when tested with more variables and the Holm-Bonferroni method adjustment. Additionally the variable weight now has a p-value of 0.0325, which is below our chosen significance cutoff of 0.05. The reason for the drop in p-value is likely caused by the presence of less variables as part of the multiple-hypothesis test. The more variables in a multiple-hypothesis test the more strict the p-value adjustment will be. With less variables our p-values are adjusted less and we end up with a significant result. So let’s have a look at our weight variable on its own now. In the command pane type the following:
estat szroeter weight
Which gives this output:

For this test we did not use a multiple-test adjustment because we are only testing one variable. If you specify the mtest() option with only one variable Stata will ignore it. This single-hypothesis test has identified monotonic heteroskedasticity in our independent variable weight. The p-value 0.0163, below our cutoff of 0.05, indicates this is statistically significant. With significant heteroskedasticity in a variable you need to decide what you are going to do next with regards to that variable. You may choose to transform the variable in some way (e.g. the natural logarithm) in order to get a more uniform variance, or you can choose to drop it from your regression model. What you decide to do will depend on whether variable transformation is appropriate for your analysis, as well as how much you know about your data.
In this example I drilled down into my estat szroeter values until I found a significant result. In a real analysis I would not recommend doing this. Even though my last test is only looking at a single variable, my previous tests were looking at multiple variables. This means in reality I was performing multiple hypothesis tests, and should therefore stick with the adjusted p-values I first obtained.
This heteroskedasticity test is more broad than that performed in estat hettest, but more specific than estat imtest. It will identify cone-shaped heteroskedasticity the same as estat hettest, however it can also identify other bendy-shaped monotonic heteroskedasticity that estat hettest would not identify. For a more general heteroskedasticity test that can look for unrestricted forms use estat imtest.