The rvfplot Command - Linear Regression Post-Estimation Plots
The rvfplot command plots the residuals against the fitted values of the dependent variable. This command is used to look for heteroskedasticity and non-linearity in a linear regression model. There should be no pattern to the residuals in this plot, they should be uniformly randomly distributed across the graph.
Any pattern to the residuals is indicative of heteroskedasticity. One of the underlying assumptions of linear regression is that of homoscedastic residuals. Any heteroskedasticity identified with this plot means your model is problematic. Additionally, if you can see a curved pattern this indicates that your dependent variable is not linear. The dependent variable needs to be broadly linear for a linear regression to be the correct model fit.
You can use this plot in conjunction with the estat hettest, estat szroeter and estat imtest commands to identify heteroskedasticity. The estat ovtest command can be used to look for non-linearity, and the graph matrix command can be used to check linear relationships between variables. You can also run a linear regression with only one independent variable to check if the relationship between two variables appears linear.
How to Use:
*Run a linear regression, then
rvfplot
OR to add a line to help identify heteroskedasticity in the plot
rvfplot, yline(0)
OR to overlay another plot onto the graph
rvfplot, addplot(plottype yvariable xvariable)
Worked Example 1:
For this example we perform a regression using the weight and trunk variables from the auto dataset. We can then plot the residuals against the fitted values with the rvfplot command to look for heteroskedasticity and non-linearity in our simple linear regression model. In the command pane I type the following:
sysuse auto, clear
regress weight trunk
rvfplot
This produces the following graph:
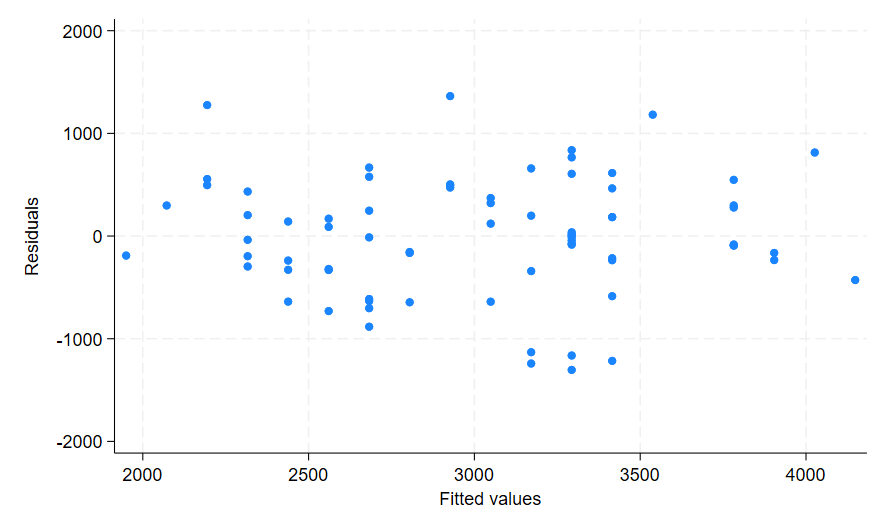
This looks pretty good. Let’s add a line to help identify any potential spatial patterns. In the command pane:
rvfplot, yline(0)

There is no obvious discernible pattern in the graph, and the plot appears evenly and randomly distributed above and below the line. I am satisfied from this that there is no significant heteroskedasticity or non-linearity present in this model.
Worked Example 2:
Now let’s have a look at a regression where there are some problems with the residuals versus fitted values plot. In this example I use the auto dataset. I will use the predict command to create the residuals and fitted values as variables so I can overlay a curved line on the rvfplot. In the command pane I type the following:
sysuse auto, clear
regress price mpg rep78
rvfplot
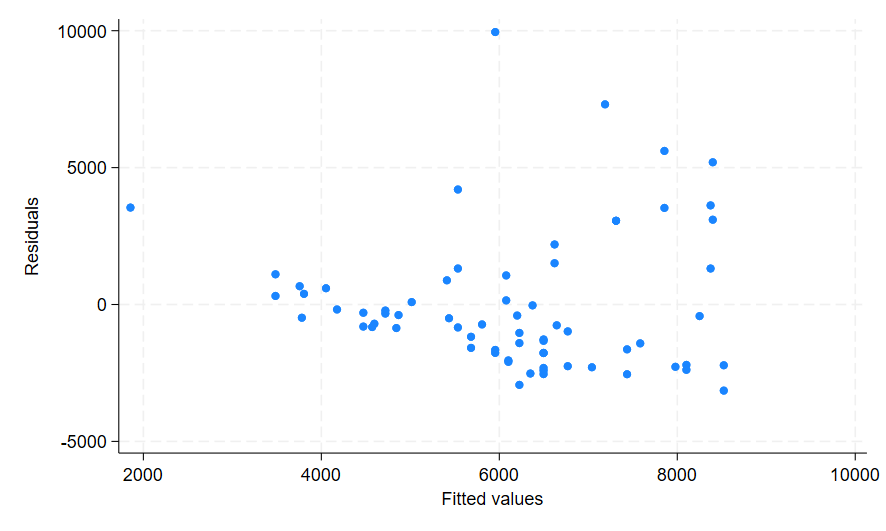
The residuals do not appear randomly distributed. Let’s add a line to confirm. In the command pane:
rvfplot, yline(0)
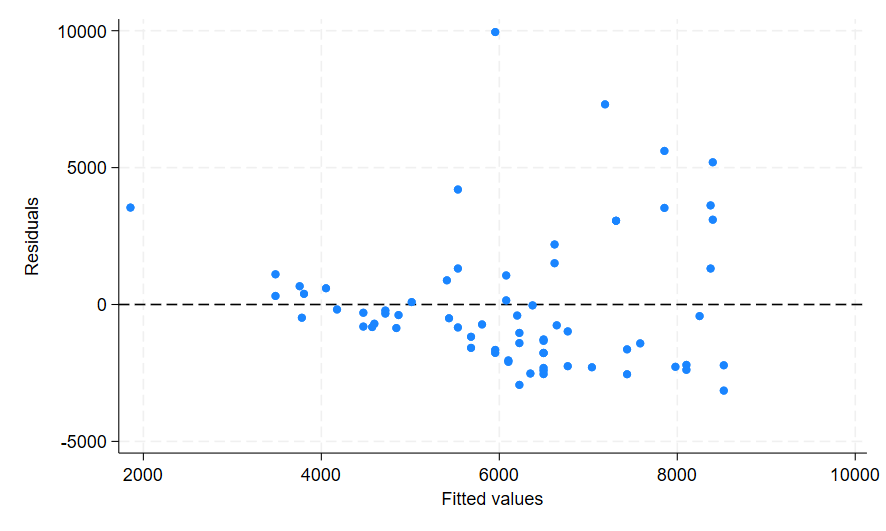
As the scatter of this plot is not uniform, it indicates heteroskedasticity in the model. The plot also appears to show a curve. Let’s fit a predicted curve to this plot to further investigate. In the command pane:
predict res, residuals
predict fitted, xb
rvfplot, addplot(qfit res fitted)

The curve does appear to fit the scatter somewhat, indicating non-linearity in the model.
Our rvfplot has indicated both non-linearity and heteroskedasticity are present in this model. We could confirm this using the estat hettest and estat imtest commands. To deal with heteroskedasticity and non-linearity in a linear regression we need to either transform one or more variables to make them more linear, or abandon a linear model altogether and look for a different model type that may fit better. In this case, since the rvfplot indicates non-linearity, I am going to perform a log transformation on the dependent variable price first to see if this has any effect. In the command pane I type the following:
drop res fitted
generate ln_price = log(price)
regress ln_price mpg rep78
predict res, residuals
predict fitted, xb
rvfplot, yline(0)
rvfplot, addplot(qfit res fitted)
This produces the following two graphs:

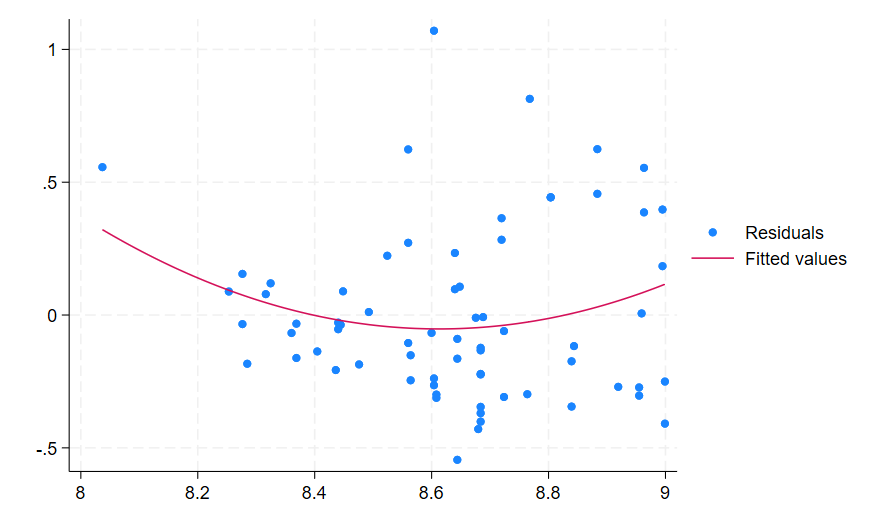
While the log transformation of the dependent variable has improved the spread of residuals somewhat, the heteroskedasticity is still present. The curved line also indicates there is still some non-linearity present. If I was particularly attached to the linear model I could continue trying different transformations, or I could try transforming a different variable. In this case however I would be inclined to look for a different model altogether, one that may better fit my chosen variables.
If you have also had a look at our estat hettest blog post, you will notice that the log transformation we performed here was enough to change the outcome of the estat hettest statistical test. While the estat hettest test indicated that the log transformation successfully dealt with the heteroskedasticity, the rvfplot we generated here indicates there is still a reasonable amount of heteroskedasticity present. One of the limitations of the estat hettest test is that it is only able to identify certain types of heteroskedasticity. This means there are other forms of heteroskedasticity that it won’t detect, and that is likely what we are seeing in our rvfplot graph. This highlights the need to perform many different diagnostic tests, both statistical and visual plots, to make sure your regression is robust.